Pythagoriciens

Les pythagoriciens étaient les disciples du philosophe-mathématicien Pythagore. Basés d'abord sur l'île de Samos, puis à Croton, dans le sud de l'Italie, ils ont été les premiers à faire la profonde découverte que tous les aspects de la nature - notes de musique, mathématiques, sciences, architecture et ingénierie - suivaient des règles déterminées par la relation entre les nombres.

Les pythagoriciens étaient comme un culte religieux ascétique. Ils croyaient en la réincarnation et pratiquaient des rituels de purification pour tenter d'effacer les fautes commises dans les vies antérieures. Ils devaient suivre de nombreuses règles. Ils devaient être végétariens, ne pouvaient pas boire de vin et devaient observer des périodes de silence. Leurs rituels de purification étaient menés dans le plus grand secret.

John Burnet a écrit dans "Early Greek Philosophy" : "L'Ordre pythagoricien était simplement, à l'origine, une fraternité religieuse, et non, comme on l'a soutenu, une ligue politique. Il n'avait pas non plus quoi que ce soit à voir avec l'"idéal aristocratique dorien". Pythagore était un Ionien, et l'Ordre était à l'origine confiné aux États achéens. De plus, l'"idéal aristocratique dorien" est une fiction basée sur la théorie de l'âge d'or.L'idéalisation socratique de Sparte et de la Crète. Corinthe, Argos et Syracuse sont tout à fait oubliées. Rien ne prouve non plus que les pythagoriciens aient favorisé le parti aristocratique. L'objectif principal de l'Ordre était de cultiver la sainteté. À cet égard, il ressemblait à une société orphique, bien qu'Apollon, et non Dionysos, soit le dieu principal des pythagoriciens. Cela est sans doute dû au lien qui existe entre l'Ordre et la société orphique.Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3rd edition, 1920, Evansville University].

Catégories avec articles apparentés dans ce site web : Philosophie et sciences grecques et romaines (33 articles) factsanddetails.com ; Religion et mythes grecs et romains (35 articles) factsanddetails.com ; Histoire de la Grèce antique (48 articles) factsanddetails.com ; Art et culture de la Grèce antique (21 articles) factsanddetails.com ; Vie, gouvernement et infrastructure de la Grèce antique (29 articles)factsanddetails.com ; Histoire de la Rome antique (34 articles) factsanddetails.com ; Histoire de la Rome antique (33 articles) factsanddetails.com ; Vie romaine (39 articles) factsanddetails.com ; Art et culture romains (33 articles) factsanddetails.com ; Gouvernement, armée, infrastructure et économie romains (42 articles) factsanddetails.com

Sites web sur la Grèce et la Rome antiques : Internet Encyclopedia of Philosophy iep.utm.edu ; Stanford Encyclopedia of Philosophy plato.stanford.edu ; Internet Ancient History Sourcebook : Greece sourcebooks.fordham.edu ; Internet Ancient History Sourcebook : Hellenistic World sourcebooks.fordham.edu ; BBC Ancient Greeks bbc.co.uk/history/ ; Musée canadien d'histoire historymuseum.ca ; Perseus Project - Tufts University ; perseus.tufts.edu; ; Gutenberg.org gutenberg.org ; British Museum ancientgreece.co.uk ; Illustrated Greek History, Dr Janice Siegel, Department of Classics, Hampden-Sydney College, Virginia hsc.edu/drjclassics ; The Greeks : Crucible of Civilization pbs.org/empires/thegreeks ; Oxford Classical Art Research Center : The Beazley Archive beazley.ox.ac.uk ; Ancient-Greek.org ancientgreece.com ; Metropolitan Museum ofArt metmuseum.org/about-the-met/curatorial-departments/greek-and-roman-art ; L'ancienne cité d'Athènes stoa.org/athens ; The Internet Classics Archive kchanson.com ; Internet Ancient History Sourcebook : Rome sourcebooks.fordham.edu ; Internet Ancient History Sourcebook : Late Antiquity sourcebooks.fordham.edu ; Forum Romanum forumromanum.org ; "Outlines of Roman History" forumromanum.org ; "TheLa vie privée des Romains" forumromanum.org

L'Empire romain au 1er siècle pbs.org/empires/romans ; The Internet Classics Archive classics.mit.edu ; Bryn Mawr Classical Review bmcr.brynmawr.edu ; De Imperatoribus Romanis : An Online Encyclopedia of Roman Emperors roman-emperors.org ; Cambridge Classics External Gateway to Humanities Resources web.archive.org/web ; Ressources sur la Rome antique pour les élèves de la Courtenay Middle SchoolBibliothèque web.archive.org ; Histoire de la Rome antique OpenCourseWare de l'Université de Notre Dame /web.archive.org ; Nations unies de Roma Victrix (UNRV) Histoire unrv.com

Pythagore de Samos (VIe siècle avant J.-C.) aurait été le premier homme à se qualifier de philosophe et serait à l'origine du mot "philosophie". Aucun de ses écrits originaux n'a survécu. Selon la légende, il aurait fui l'île égéenne de Samos dans sa jeunesse pour échapper à un tyran maléfique. Après avoir été exposé à de nouvelles idées en Égypte et en Asie mineure, il a fondé une école dans la colonie italienne deKroton en 530 avant J.-C. Après avoir été persécuté et contraint de fuir à nouveau, il s'est installé à Metapontum, en Grèce, où il est mort vers 500 avant J.-C..

Pythagore dans l'histoire de la philosophie de Thomas Stanley

Pythagore a été l'une des premières personnes à devenir végétarienne pour des raisons de santé et de philosophie. Il mangeait du pain et du miel pour ses repas, avec des légumes en dessert, et il s'abstenait même de manger des œufs et des haricots. Il ne mangeait pas de viande parce qu'il croyait que les animaux avaient une âme. Sa croyance à propos des haricots n'avait rien à voir avec les pets. Elle était plutôt basée sur la croyance que les haricots étaient la première progéniture...de la Terre.

Il n'existe aucune preuve que Pythagore ait été mathématicien, et encore moins qu'il ait démontré le théorème qui porte son nom ou qu'il ait découvert les rapports des intervalles musicaux. Il était cependant un adorateur des nombres et un gourou qui a fondé une commune et a parlé de la venue d'une figure messianique. Le théorème qui porte son nom ("la somme de l'hypoténuse d'un triangle rectangle est égale à la somme des carrés des deux autres triangles") a été écrit par Pythagore.côtés") était connu des Sumériens dès 2000 avant Jésus-Christ.

"On peut dire avec certitude que Pythagore a passé ses premières années d'âge adulte à Samos, qu'il était le fils de Mnesarchus et qu'il a "prospéré", nous dit-on, sous le règne de Polycrate (532 av. J.-C.). Cette date ne peut être erronée, car Héraclite parle déjà de lui au passé. Les vastes voyages attribués à Pythagore par les auteurs tardifs sont, bien sûr, apocryphes. Même l'affirmation selon laquelle il aurait fait des voyages à l'étranger n'est pas vraie.Hérodote, il est vrai, observe que les Egyptiens s'accordaient sur certaines pratiques avec les règles dites orphiques et bacchiques, qui sont réellement égyptiennes, et avec les pythagoriciens ; mais cela n'implique pas que les pythagoriciens aient dérivé directement de ces règles.Il dit aussi que la croyance en la transmigration est venue d'Égypte, bien que certains Grecs, à une date antérieure et postérieure, l'aient fait passer pour la leur. Il refuse cependant de donner leurs noms, et il ne peut donc guère faire allusion à Pythagore. Peu importe, car les Égyptiens ne croyaient pas du tout à la transmigration, et Hérodote a été trompé par les prêtres ou par le symbolisme de l'église.Source : John Burnet (1863-1928), "Early Greek Philosophy" Londres et Édimbourg : A. et C. Black, 1892, 3e édition, 1920, Université d'Evansville].

"Aristoxène dit que Pythagore quitta Samos pour échapper à la tyrannie de Polycrate. C'est à Croton, une ville qui était depuis longtemps en relations amicales avec Samos et qui était célèbre pour ses athlètes et ses médecins, qu'il fonda sa société. Timée semble avoir dit qu'il vint en Italie en 529 avant J.-C. et resta à Croton pendant vingt ans. Il mourut à Metapontum, où il s'était retiré.quand les Crotoniates se sont révoltés contre son autorité.

"Il n'est pas facile de donner un récit de Pythagore qui puisse prétendre à être considéré comme historique. La plus ancienne référence à lui, en effet, est pratiquement contemporaine. On cite quelques vers de Xénophane, dans lesquels il est dit que Pythagore entendit un jour un chien hurler et demanda à son maître de ne pas le battre, car il reconnaissait la voix d'un ami disparu. Nous savons ainsi qu'il enseigna leHéraclite, à la génération suivante, dit qu'il a poussé la recherche scientifique (historiê) plus loin que quiconque, bien qu'il s'en soit servi à des fins d'imposture. Plus tard, mais toujours au cours du siècle, Hérodote parle de lui comme de "l'homme scientifique (sophistês) le plus faible parmi les Hellènes", et il dit que les Grecs de l'Hellespont lui avaient dit quele légendaire Scythe Salmoxis avait été un esclave de Pythagore à Samos. Il ne croit pas cela, car il sait que Salmoxis a vécu de nombreuses années avant Pythagore. L'histoire, cependant, est la preuve que Pythagore était bien connu au cinquième siècle, à la fois comme homme scientifique et comme prédicateur de l'immortalité. Cela nous mène un peu plus loin. [Source : John Burnet (1863-1928), "Early Greek Philosophy" London andÉdimbourg : A. et C. Black, 1892, 3e édition, 1920, Université d'Evansville ].

Pythagore est l'école d'Athènes de Raphaël

"Platon était profondément intéressé par le pythagorisme, mais il est curieusement réservé à l'égard de Pythagore. Il ne le mentionne qu'une seule fois par son nom dans tous ses écrits, et tout ce qu'on nous dit alors est qu'il a gagné l'affection de ses disciples à un degré inhabituel (diapherontôs êgapêthê) en leur enseignant un "mode de vie", qui était encore appelé pythagoricien. Même les pythagoriciens ne sont mentionnés qu'une seule fois par leur nom, dans leoù Socrate est amené à dire qu'ils considèrent la musique et l'astronomie comme des sciences sœurs. D'autre part, Platon nous parle longuement d'hommes dont nous savons, par d'autres sources, qu'ils étaient pythagoriciens, mais il évite de les nommer. Pour autant qu'il le dise, nous devrions seulement être en mesure de deviner qu'Echecrates et Philolaus appartenaient à l'école. Habituellement, les opinions pythagoriciennes sont données de manière anonyme, comme le montrent les exemples suivantsOn ne nous dit même pas expressément que Timée le Locrien, dans la bouche duquel Platon a mis une cosmologie indubitablement pythagoricienne, appartenait à cette société ; nous devons le déduire du fait qu'il est originaire d'Italie. Aristote imite la réserve de son maître à ce sujet. Le nom de Pythagore n'apparaît que deux fois dans les œuvres authentiques.Dans un endroit, on nous dit qu'Alcmaeon était un jeune homme dans la vieillesse de Pythagore, et l'autre est une citation d'Alcidamas à l'effet que "les hommes d'Italie honoraient Pythagore". Aristote n'est pas aussi timide du mot "pythagoricien" que Platon, mais il l'utilise d'une manière curieuse. Il dit des choses telles que "les hommes d'Italie qui sont appelés pythagoriciens", et il se réfère habituellement à des mots comme "Pythagore" ou "Pythagore".Il semble qu'il y avait un certain doute au quatrième siècle quant à l'identité des véritables pythagoriciens. Nous verrons pourquoi en poursuivant.

"Aristote a aussi écrit un traité spécial sur les pythagoriciens qui n'est pas parvenu jusqu'à nous, mais dont on trouve des citations chez les auteurs postérieurs, et qui sont d'une grande valeur, car elles ont trait au côté religieux du pythagorisme.

"Le récit de l'ordre pythagoricien dans la Vie de Pythagore de Iamblique est basé principalement sur Timée, qui était sans doute un historien peu critique, mais qui avait accès à des informations sur l'Italie et la Sicile.ce qui rend son témoignage très précieux lorsqu'il peut être récupéré. Aristoxenus avait personnellement connu la dernière génération de la société pythagoricienne de Phlius. Il est évident, cependant, qu'il a voulu représenter Pythagore simplement comme un homme de science, et a été soucieux de réfuter l'idée qu'il était un enseignant religieux. De la même manière, Dicaearchus a essayé de faire croire que Pythagore était un homme de science.simplement un homme d'État et un réformateur.

"Lorsque nous en arrivons aux Vies de Pythagore, de Porphyre, d'Iamblique et de Diogène Laertius, nous nous trouvons une fois de plus dans la région du miraculeux. Elles sont basées sur des autorités de caractère très suspect, et le résultat est une masse de fiction incroyable. Il serait cependant tout à fait erroné d'ignorer les éléments miraculeux de la légende de Pythagore, car certains des miracles les plus frappants sont les suivantsLe fait est que les récits les plus anciens et les plus récents s'accordent pour représenter Pythagore comme un thaumaturge ; mais, pour une raison ou une autre, on a tenté au quatrième siècle de sauver sa mémoire de cette influence.Cela permet d'expliquer les références prudentes de Platon et d'Aristote, mais sa pleine signification n'apparaîtra que plus tard.

"Pendant un certain temps, le nouvel ordre réussit à s'assurer le pouvoir suprême dans les cités achéennes, mais la réaction ne tarde pas à venir. Nos comptes rendus de ces événements sont très confus parce que nous ne faisons pas la distinction entre la révolte de Cylon, du vivant de Pythagore lui-même, et les soulèvements ultérieurs qui ont conduit à l'expulsion des Pythagoriciens d'Italie. Ce n'est que si nous les séparons que nous commençons à voir notre chemin.Timée semble avoir lié étroitement le soulèvement de Cylon aux événements qui ont conduit à la destruction de Sybaris (510 av. J.-C.) [Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3rd edition, 1920, Evansville University].

"Nous en déduisons que Pythagore avait, d'une manière ou d'une autre, manifesté de la sympathie pour les Sybarites et avait exhorté les habitants de Croton à accueillir certains réfugiés qui avaient été expulsés par le tyran Telys. Rien ne permet d'affirmer qu'il a sympathisé avec ces réfugiés parce qu'ils étaient des "aristocrates" ; ils étaient victimes d'un tyran et de suppliants, et il n'est pas difficile de comprendre que l'ionien PythagoreCylon, dont Aristoxenus dit expressément qu'il était l'un des premiers hommes de Croton en termes de richesse et de naissance, a pu faire en sorte que Pythagore se retire à Metapontum, une autre ville achéenne, et c'est là qu'il a passé ses dernières années.

"Les troubles continuèrent cependant à Croton après le départ de Pythagore pour le Métaponte et après sa mort. Enfin, nous dit-on, les Cyloniens mirent le feu à la maison de l'athlète Milo, où les Pythagoriciens étaient rassemblés. De ceux qui se trouvaient dans la maison, deux seulement, qui étaient jeunes et forts, Archippe et Lysis, échappèrent. Archippe se retira à Taras, un État démocratique dorien : Lysis, d'abord àIl est impossible de dater ces événements avec précision, mais la mention de Lysis prouve qu'ils se sont étalés sur plus d'une génération. Le coup d'État de Croton ne peut guère s'être produit avant 450 av. J.-C., si le professeur d'Epaminondas y a échappé, et il ne peut pas non plus être beaucoup plus tardif, sinon nous en aurions entendu parler dans les années 1980.Dans un passage précieux, sans doute dérivé de Timée, Polybe nous parle de l'incendie des "loges" pythagoriciennes (sunedria) dans toutes les cités achéennes, et la façon dont il parle suggère que cela a duré un temps considérable, jusqu'à ce que finalement la paix et l'ordre soient rétablis par les Achéens du Péloponnèse.A ce jour, certains pythagoriciens ont pu retourner en Italie, où ils ont à nouveau acquis une grande influence."

"Après avoir perdu leur suprématie dans les cités achéennes, les pythagoriciens se concentrèrent à Rhégion ; mais l'école qui y avait été fondée ne se maintint pas longtemps, et seul Archytas resta en Italie. Philolaus et Lysis, ce dernier ayant échappé tout jeune au massacre de Croton, avaient déjà trouvé le chemin de Thèbes. Nous savons par Platon que Philolaus s'y trouvait versà la fin du Ve siècle, et Lysis fut ensuite le professeur d'Epaminondas. Certains pythagoriciens purent cependant retourner en Italie plus tard. Philolaus le fit certainement, et Platon laisse entendre qu'il avait quitté Thèbes quelque temps avant 399 avant J.-C., l'année de la mise à mort de Socrate. Au IVe siècle, le siège principal de l'école est la ville dorienne de Taras, et nous trouvons les pythagoriciensC'est à cette période qu'appartient l'activité d'Archytas. Ami de Platon, il a presque réalisé l'idéal du roi philosophe. Il a régné sur Taras pendant des années, et Aristoxenus nous dit qu'il n'a jamais été vaincu sur le champ de bataille. Il a également été l'inventeur de la mécanique mathématique. À la même époque, le pythagorisme s'était enraciné dans le pays.Est. Lysis resta à Thèbes, où Simmias et Cébès avaient entendu Philolaus, tandis que le reste de l'école pythagoricienne de Rhégion s'installa à Phlius.

Pythagore et Philolaus

"Des opinions de Pythagore, nous savons encore moins que de sa vie. Platon et Aristote ne savaient manifestement rien de certain des doctrines éthiques ou physiques remontant au fondateur lui-même. Aristoxène a donné une série de préceptes moraux. Dicée a dit qu'on ne connaissait pratiquement rien de ce que Pythagore enseignait à ses disciples, sauf la doctrine de la transmigration, le cycle périodique et la parenté de tous lesPythagore préférait apparemment l'enseignement oral à la diffusion de ses opinions par l'écriture, et ce n'est qu'à l'époque alexandrine que quelqu'un s'est aventuré à forger des livres en son nom. Les écrits attribués aux premiers pythagoriciens étaient également des faux de la même époque. L'histoire primitive du pythagorisme est donc entièrement conjecturale, mais nous pouvons tout de même tenter d'en faire la synthèse.comprendre, de manière très générale, quelle a dû être la position de Pythagore dans l'histoire de la pensée grecque [Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3rd edition, 1920, Evansville University].

Philolaus (470-ca. 385 av. J.-C.) de Croton, dans le sud de l'Italie - un philosophe-scientifique grec et contemporain de Socrate - a été l'un des principaux artisans des enseignements pythagoriciens. Selon la Stanford Encyclopedia of Philosophy, "il est l'une des trois figures les plus importantes de la tradition pythagoricienne, né cent ans après Pythagore lui-même et cinquante ans avant Archytas. Il a écritun livre, Sur la nature, qui était probablement le premier livre écrit par un pythagoricien. Il y a eu une controverse considérable concernant les 20+ fragments qui ont été conservés au nom de Philolaus. Il est maintenant généralement accepté que quelque onze des fragments proviennent de son livre authentique."

Il semble naturel de supposer que les éléments pythagoriciens du Phédon et du Gorgias de Platon proviennent principalement de Philolaus. Platon fait en sorte que Socrate s'étonne que Simmias et Cébès n'aient pas appris de lui pourquoi il est illégal pour un homme de s'ôter la vie, et il semble sous-entendre que les pythagoriciens de Thèbes utilisaient le mot "philosophe" dans le sens particulier d'un homme qui cherche à trouver un moyen d'échapper à la mort.Il est probable que Philolaus parlait du corps (sôma) comme de la tombe (sêma) de l'âme. Nous sommes donc fondés à penser qu'il enseignait l'ancienne doctrine religieuse pythagoricienne sous une forme ou une autre et qu'il insistait particulièrement sur la connaissance comme moyen de libération. C'est l'impression que nous donne Platon, qui est de loin la meilleure autorité que nous ayons. [Source : JeanBurnet (1863-1928), " Early Greek Philosophy " Londres et Edimbourg : A. et C. Black, 1892, 3e édition, 1920, Université d'Evansville ].

" Nous savons en outre que Philolaus a écrit sur les " nombres " ; car Speusippus l'a suivi dans l'exposé qu'il a fait des théories pythagoriciennes sur ce sujet. Il est probable qu'il s'occupait surtout d'arithmétique, et nous ne pouvons guère douter que sa géométrie était du type primitif décrit dans un chapitre précédent. Eurytus était son disciple, et nous avons vu que ses vues étaient encore très grossières.

"Nous savons maintenant que Philolaus a écrit sur la médecine et que, bien qu'apparemment influencé par les théories de l'école sicilienne, il s'y opposait du point de vue pythagoricien. En particulier, il disait que notre corps n'était composé que de chaud et ne participait pas au froid. Ce n'est qu'après la naissance que le froid était introduit par la respiration. Le lien de ceci avec l'ancienLa théorie pythagoricienne est claire : de même que le Feu dans le macrocosme aspire et limite le souffle froid et sombre qui entoure le monde, de même notre corps aspire le souffle froid du dehors. Philolaus a fait de la bile, du sang et du flegme les causes de la maladie ; et, conformément à cette théorie, il a dû nier que le flegme soit froid, comme le soutenait l'école sicilienne. Son étymologie prouvait qu'il était chaud. Nous verrons queque c'est probablement cette préoccupation pour la médecine de l'école sicilienne qui a donné lieu à certains des développements les plus frappants du pythagorisme ultérieur.

Les pythagoriciens croyaient à l'immortalité et à la "transmigration de l'âme" (l'idée qu'après la mort les âmes allaient au ciel ou occupaient des corps d'hommes ou d'animaux). Ils pensaient également que la connaissance pure était l'essence de l'âme et que le meilleur moyen d'atteindre la connaissance pure était les nombres.

Pythagore sortant des Enfers

Pythagore aurait enseigné la doctrine de la transmigration. Certains spécialistes affirment que cette croyance s'explique le plus facilement comme un développement de la vision de la parenté des hommes et des bêtes, une vision que Dicée disait être celle de Pythagore. De plus, cette croyance est communément associée à un système d'interdits sur certains types de nourriture, et la règle pythagoricienne est surtout connue pour sa prescription d'interdits similaires.Il semble certain que Pythagore l'a apporté avec lui d'Ionie. Timée raconte qu'à Délos, il refusait de sacrifier sur tout autre autel que le plus ancien, celui d'Apollon le Père, où seuls les sacrifices non sanglants étaient autorisés. [Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3e édition, 1920, Evansville University].

Diogène Laertius (180-240) a écrit : "Sur le sujet de la réincarnation, Xénophane témoigne dans une élégie qui commence par "Je vais maintenant passer à un autre conte et montrer le chemin". Ce qu'il dit de Pythagore est le suivant : On raconte qu'il passait par là lorsqu'un chiot était fouetté, et qu'il eut pitié et dit : "Arrête, ne le frappe pas. Car c'est l'âme d'un ami que j'ai reconnue quand je l'ai entenduedonner sa langue." [Source : Diogène Laertius, 8. 36)

Hérodote (c. 484-c. 425 av. J.-C.) a écrit dans les Histoires II. 123 : "Les Égyptiens sont les premiers à avoir soutenu la doctrine selon laquelle l'âme de l'homme est immortelle, et que lorsque le corps périt, il entre dans un autre animal qui naît à ce moment-là, et lorsqu'il a fait le tour complet des créatures de la terre ferme, de la mer et de l'air, il entre à nouveau dans le corps d'un homme".à la naissance. Et son cycle s'achève en 3000 ans. Il y a des Grecs qui ont adopté cette doctrine, certains dans le passé, d'autres plus tard, comme si c'était leur propre invention. Je connais leurs noms, mais je m'abstiens de les écrire."

Porphyrius écrit dans la Vie de Pythagore 19 : "Néanmoins, ce qui suit est devenu universellement connu : premièrement, qu'il soutient que l'âme est immortelle ; deuxièmement, qu'elle se transforme en d'autres sortes d'êtres vivants ; troisièmement, que les événements se reproduisent dans certains cycles et que rien n'est jamais absolument nouveau ; et quatrièmement, que tous les êtres vivants doivent être considérés comme apparentés.d'apporter ces croyances en Grèce."

Les pythagoriciens croyaient en une interdiction générale de manger des animaux au motif qu'ils avaient "le droit de vivre en commun avec l'humanité". Leurs idées ont inspiré les néoplatoniciens des troisième et quatrième siècles de notre ère et leurs vues sur la purification de l'âme avant la vie après la mort ont influencé les premiers chrétiens.

Il y a deux opinions sur les règles pythagoriciennes, chacune provenant de "sources différentes". Certaines d'entre elles, dérivées d'Aristoxenus et conservées pour la plupart par Iamblichus, sont de simples préceptes de moralité. Elles ne prétendent pas remonter à Pythagore lui-même ; ce ne sont que des dictons que la dernière génération de "mathématiciens" a entendus de leurs prédécesseurs. La seconde classe est d'une nature différente, etIl s'agit de règles appelées Akousmata, ce qui indique qu'elles étaient la propriété de la secte qui avait fidèlement conservé les anciennes coutumes. Les auteurs ultérieurs les interprètent comme des "symboles" de la vérité morale, mais il n'est pas nécessaire d'avoir l'œil exercé pour voir qu'il s'agit de véritables tabous. [Source : John Burnet (1863-1928), "Early Greek Philosophy" Londres et Édimbourg : A. et C. Black, 1892, 3e édition, 1920,Université d'Evansville ]

Ne pas manger de haricots

"Je donne quelques exemples pour montrer ce qu'était réellement la règle de Pythagore.

1. s'abstenir de consommer des haricots.

2. ne pas ramasser ce qui est tombé.

3. Ne pas toucher une bite blanche.

4. ne pas rompre le pain.

5. ne pas enjamber une barre transversale.

6) Ne pas remuer le feu avec le fer.

7. ne pas manger d'un pain entier.

8. de ne pas cueillir une guirlande.

9. ne pas s'asseoir sur une mesure à quart de litre.

10. Ne pas manger le cœur.

11. de ne pas marcher sur les autoroutes.

12. ne pas laisser les hirondelles partager son toit.

13) Quand on retire la marmite du feu, ne pas en laisser la trace dans les cendres, mais les remuer ensemble.

14. ne pas se regarder dans un miroir à côté d'une lumière.

15. quand tu te lèves, roule les draps et lisse l'impression du corps.

Hérodote (c. 484-c. 425 av. J.-C.) écrit dans les Histoires II. 81 : "Mais les articles en laine ne sont jamais apportés dans les temples, et on ne les enterre pas avec (les Égyptiens). Ce n'est pas licite. Ils sont d'accord en cela avec les pratiques dites orphiques et bacchiques (qui sont vraiment égyptiennes) et avec les pythagoriciens. Car il n'est pas licite pour quelqu'un qui participe à ces rites d'être enterré avec des vêtements en laine. Il y a un sacrécompte rendu donné sur ce sujet."

Diogène Laertius (180-240 apr. J.-C.) a écrit : "Par-dessus tout, (Pythagore) interdisait de manger du rouget et de la queue noire. Il exigeait l'abstinence de cœur et de haricots. Il sacrifiait aussi (selon Aristote), en certaines occasions, du ventre de la mère et du rouget.... Il ne sacrifiait que des choses inanimées. Mais d'autres disent qu'il n'utilisait que des coqs, des chevreaux de lait et des porcelets, et jamais d'agneaux." [Source :Diogène Laertius 8. 19]

"On a en effet douté que nous puissions accepter ce que nous disent des auteurs tardifs comme Porphyre au sujet de l'abstinence pythagoricienne. Aristoxenus a sans doute dit que Pythagore ne s'abstenait pas de la chair animale en général, mais seulement de celle du bœuf de labour et du bélier. Il a aussi dit que Pythagore préférait les haricots à tout autre légume, comme étant les plus laxatifs, et qu'il étaitL'exagération palpable de ces déclarations montre cependant qu'il s'efforce de combattre une croyance qui existait à son époque, et nous pouvons ainsi démontrer, de sa propre bouche, que la tradition qui faisait que les pythagoriciens s'abstenaient de la chair animale et des haricots remontait à une époque bien antérieure aux néopythagoriciens. L'explication est qu'Aristoxenus avait été le chef de la communauté des pythagoriciens.Les "pythagoristes" qui s'accrochaient aux anciennes pratiques étaient maintenant considérés comme des hérétiques, et l'on disait que les Akousmatics, comme on les appelait, étaient en réalité des disciples d'Hippasus, qui avait été excommunié pour avoir révélé des informations secrètes.Les véritables disciples de Pythagore étaient les mathématiciens. La satire des poètes de la Comédie du Milieu prouve cependant que, même si les amis d'Aristoxène ne pratiquaient pas l'abstinence, il y avait au IVe siècle beaucoup de gens qui se disaient disciples de Pythagore. Nous savons aussi par Isocrate qu'ils observaient encore la règle du silence. L'histoire a montré qu'il n'y avait pas d'autre solution que d'observer le silence.Les noms de Diodore d'Aspendus et de Nigidius Figulus aident à combler le fossé entre eux et Apollonius de Tyane.

"Nous avons vu que Pythagore enseignait la parenté des bêtes et des hommes, et nous en déduisons que sa règle d'abstinence de chair était fondée, non pas sur des motifs humanitaires ou ascétiques, mais sur un tabou. Cela est confirmé de manière frappante par une déclaration de Porphyre dans sa Défense de l'abstinence, selon laquelle, bien que les Pythagoriciens se soient généralement abstenus de chair, ils en mangeaient néanmoins lorsqu'ils sacrifiaient à l'Eternel.Or, chez les peuples primitifs, nous constatons souvent que l'animal sacré est tué et mangé dans certaines occasions solennelles, alors que, dans des circonstances ordinaires, ce serait la plus grande des impiétés. Ici encore, nous avons une croyance primitive, et nous n'avons pas besoin d'attacher de poids aux dénégations d'Aristoxène.

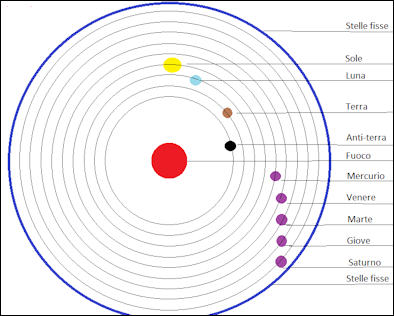
La vision pythagoricienne de l'univers

Les pythagoriciens croyaient que le monde était une sphère et que la sphère était la forme la plus parfaite. Ils ont ensuite poussé cette idée un peu plus loin, en théorisant que la Terre était le centre de l'univers, car tous les objets sont attirés vers le centre de quelque chose, ce qui crée une sphère (dans ce cas, la Terre).

"La déclaration la plus frappante de ce genre est celle d'Aristote. Les Pythagoriciens soutenaient, nous dit-il, qu'il y avait un "souffle sans limite" en dehors des cieux, et qu'il était inhalé par le monde. En substance, c'est la doctrine d'Anaximène, et il devient pratiquement certain qu'elle a été enseignée par Pythagore, lorsque nous constatons que Xénophane l'a niée. Nous pouvons en déduire que le développement ultérieur de la doctrine de Pythagore a été très important.On nous dit qu'après la formation de la première unité - quelle que soit la manière dont cela s'est produit - la partie la plus proche de l'illimité a été aspirée et limitée ; et que c'est l'illimité ainsi aspiré qui maintient les unités séparées les unes des autres. Il représente l'intervalle entre elles. C'est une manière primitive de décrire une quantité discrète.

"Dans ces passages d'Aristote, le "souffle" est également désigné comme le vide ou la vacuité. C'est une confusion que nous avons déjà rencontrée chez Anaximène, et nous ne devons pas nous étonner de la retrouver ici. Nous trouvons également des traces claires de l'autre confusion, celle de l'air et de la vapeur. Il semble certain, en effet, que Pythagore identifiait la limite avec le feu, et l'illimité avec les ténèbres. Aristote nous ditque Hippasus a fait du Feu le premier principe, et nous verrons que Parménide, en discutant les opinions de ses contemporains, leur attribue l'idée qu'il y avait deux "formes" primaires, le Feu et la Nuit. Nous constatons également que la Lumière et les Ténèbres apparaissent dans la table pythagoricienne des opposés sous les titres de la Limite et de l'Illimité respectivement. L'identification du souffle avec les ténèbres iciCe qui est sous-entendu est une forte preuve du caractère primitif de la doctrine ; en effet, au sixième siècle, les ténèbres étaient supposées être une sorte de vapeur, alors qu'au cinquième, leur véritable nature était connue. Platon, avec son habituel tact historique, fait décrire au Timée pythagoricien la brume et les ténèbres comme de l'air condensé. Il faut donc penser à un "champ" de ténèbres ou de souffle délimité par des unités lumineuses, à une imaginationIl est même probable que nous devrions attribuer à Pythagore l'opinion milésienne d'une pluralité de mondes, bien qu'il n'eût pas été naturel qu'il parlât d'un nombre infini. Nous savons, du moins, que Pétron, l'un des premiers pythagoriciens, disait qu'il n'y avait que cent quatre-vingt-trois mondes disposés en triangle.

"Anaximandre avait considéré les corps célestes comme des roues d'"air" remplies de feu qui s'échappe par certains orifices (§ 21), et il est prouvé que Pythagore a adopté la même vue. Nous avons vu qu'Anaximandre ne supposait l'existence que de trois roues de ce type, et il est extrêmement probable que Pythagore a identifié les intervalles entre celles-ci avec les trois intervalles musicaux qu'il avaitCe serait le début le plus naturel pour la doctrine de "l'harmonie des sphères", bien que l'expression serait doublement trompeuse si elle était appliquée à une théorie que nous pouvons correctement attribuer à Pythagore lui-même. Le mot harmonia ne signifie pas harmonie, mais octave, et les "sphères" sont un anachronisme. Nous en sommes encore au stade où les roues ou les anneaux sont utilisés.étaient considérés comme suffisants pour rendre compte des corps célestes.

"La distinction entre la révolution diurne des cieux d'est en ouest, et les révolutions plus lentes du soleil, de la lune et des planètes d'ouest en est, peut également être attribuée aux premiers temps de l'école, et probablement à Pythagore lui-même. Elle implique évidemment une rupture complète avec la théorie du tourbillon, et suggère que les cieux sont sphériques. C'était cependant la seule façon d'obtenir des résultats.Si l'on veut le prendre au sérieux, il faut supposer que les mouvements du soleil, de la lune et des planètes sont composites. D'une part, ils ont leurs propres révolutions avec des vitesses angulaires variables d'ouest en est, mais ils sont également entraînés par la révolution diurne d'est en ouest. Apparemment, cela a été exprimé en disant que les mouvements du soleil, de la lune et des planètes sont composites.les orbites planétaires, qui sont obliques par rapport à l'équateur céleste, sont maîtrisées (krateitai) par la révolution diurne. Les Ioniens, jusqu'à l'époque de Démocrite, n'ont jamais accepté cette conception. Ils s'en tenaient à la théorie du tourbillon, qui obligeait à considérer que tous les corps célestes tournaient dans le même sens, de sorte que ceux qui, dans le système pythagoricien, ont la plus grande vitesse angulaireSelon la vision pythagoricienne, Saturne, par exemple, prend environ trente ans pour accomplir sa révolution ; selon la vision ionienne, elle est "laissée en arrière" bien moins que n'importe quelle autre planète, c'est-à-dire qu'elle suit plus fidèlement le rythme des signes du Zodiaque.

" Pour des raisons qui apparaîtront plus tard, nous pouvons avec confiance attribuer à Pythagore lui-même la découverte de la sphéricité de la terre, que les Ioniens, même Anaxagore et Démocrite, refusaient d'accepter. Il est probable, cependant, qu'il adhérait encore au système géocentrique, et que la découverte que la terre était une planète appartient à une génération ultérieure (§ 150).

"L'exposé qui vient d'être fait des vues de Pythagore est, sans doute, conjectural et incomplet. Nous lui avons simplement attribué les parties du système pythagoricien qui paraissent les plus anciennes, et il n'a même pas été possible, à ce stade, de citer complètement les preuves sur lesquelles repose notre discussion. Celle-ci n'apparaîtra sous son vrai jour que lorsque nous aurons examiné la deuxième partie du poème deIl est clair, en tout cas, que la grande contribution de Pythagore à la science a été sa découverte que les intervalles concordants pouvaient être exprimés par de simples rapports numériques. En principe, du moins, cela suggère une vision entièrement nouvelle de la relation entre les "opposés" traditionnels. Si un accord parfait (harmonia) entre le haut et le bas peut être obtenu par le biais d'un système d'échange d'informations, il n'y a pas de problème.Le chaud et le froid, l'humide et le sec, peuvent être unis dans un juste mélange (krasis), une idée dont témoigne encore notre mot "température". La doctrine médicale des "tempéraments" est dérivée de la même source. De plus, la célèbre doctrine de la moyenne n'est qu'une application du même principe.Il n'est pas exagéré de dire que la philosophie grecque sera désormais dominée par la notion de corde parfaitement accordée.

"S'il n'y avait que cela, nous serions tentés d'effacer le nom de Pythagore de l'histoire de la philosophie, et de le reléguer dans la classe des "hommes-médecine" (goêtes) avec Epiménide et Onomacrite. Mais ce serait une erreur. La société pythagoricienne devint la principale école scientifique de la Grèce, et il est certain que la science pythagoricienne remonte aux premières années du Ve siècle.Héraclite, qui n'est pas tendre avec lui, dit que Pythagore avait poursuivi la recherche scientifique plus loin que d'autres hommes. Hérodote a appelé Pythagore "non pas le plus faible sophiste des Hellènes", un titre qui, à cette date, n'implique pas le moindre dénigrement, mais implique des études scientifiques. Aristote dit que Pythagore s'est d'abord occupé de la recherche scientifique et de l'éducation.Peut-on trouver un lien entre ces deux aspects de son activité ? [Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3rd edition, 1920, Evansville University].

"Nous avons vu que le but des Orphes et d'autres Orgies était d'obtenir la libération de la "roue de la naissance" au moyen de "purifications" d'un type primitif. La nouveauté de la société fondée par Pythagore semble avoir été que, tout en admettant toutes ces anciennes pratiques, elle suggérait en même temps une idée plus profonde de ce qu'est réellement la "purification". Aristoxène dit que les Pythagoriciens employaientCes méthodes de purification de l'âme étaient familières dans l'Orgia des Korybantes, et servent à expliquer l'intérêt des pythagoriciens pour les harmoniques. Mais il y a plus que cela. Si nous pouvons nous fier à Héraclide, c'est Pythagore qui a été le premier à distinguer les "trois vies", la Théorique, la Pratique et l'Apolaïque, qu'Aristote a fait de l'Harmonie.dans l'éthique.

La doctrine est la suivante : nous sommes étrangers en ce monde, et le corps est le tombeau de l'âme, et pourtant nous ne devons pas chercher à nous échapper par le meurtre de nous-mêmes ; car nous sommes les biens de Dieu qui est notre gardien, et sans son ordre nous n'avons pas le droit de nous échapper. Dans cette vie, il y a trois sortes d'hommes, comme il y a trois sortes de personnes qui viennent aux Jeux olympiques. La classe la plus basse est celle des enfants.La plus grande purification de toutes est donc la science, et c'est l'homme qui s'y consacre, le vrai philosophe, qui s'est le plus efficacement libéré de la "roue de la naissance". Il serait téméraire de dire que Pythagore a été le premier à se rendre compte de l'importance de la science dans l'histoire de l'humanité.Il est facile de comprendre que la plupart de ses disciples se sont contentés des formes de purification les plus humbles, et c'est ce qui explique la secte des Akousmatics.Quelques-uns s'élevèrent jusqu'à la doctrine supérieure, et nous devons maintenant nous demander quelle part de la science pythagoricienne ultérieure peut être attribuée à Pythagore lui-même.

Proclus (412-485 ap. J.-C.) a écrit : "Ainsi, Pythagore a fait de la philosophie géométrique une forme d'éducation libérale en recherchant ses premiers principes dans un royaume supérieur de réalité...." [Source : Proclus In Eucl. p. 65 Friedlander].

"Dans son traité sur l'Arithmétique, Aristoxenus dit que Pythagore fut le premier à porter cette étude au-delà des besoins du commerce, et son affirmation est confirmée par tout ce que nous savons par ailleurs. A la fin du cinquième siècle avant J.-C., nous constatons qu'il y a un intérêt répandu pour de tels sujets et que ceux-ci sont étudiés pour eux-mêmes. Or, ce nouvel intérêt ne peut pas être entièrement le fait d'une seule personne.Mais comme il n'a rien écrit, nous n'avons aucun moyen sûr de distinguer son propre enseignement de celui de ses disciples de la génération ou des deux générations suivantes. Tout ce que nous pouvons dire avec certitude, c'est que plus une doctrine pythagoricienne paraît primitive, plus il est probable qu'elle soit celle de Pythagore lui-même,En particulier, lorsque nous constatons que les pythagoriciens postérieurs enseignent des choses qui étaient déjà quelque peu anachroniques à leur époque, nous pouvons être pratiquement sûrs que nous avons affaire à des survivances que seule l'autorité du nom du maître pouvait préserver.Ce n'est qu'en séparant sa forme la plus ancienne de sa forme la plus tardive que la place du pythagorisme dans la pensée grecque peut être clarifiée, bien que nous devions nous rappeler que personne ne peut prétendre aujourd'hui tracer avec certitude la ligne de démarcation entre ses étapes successives [Source : John Burnet (1863-1928), "Early GreekPhilosophy" Londres et Edimbourg : A. et C. Black, 1892, 3e édition, 1920, Université d'Evansville ].

Pythagore et Euclide

"L'une des déclarations les plus remarquables que nous ayons sur le pythagorisme est ce que l'on nous dit d'Eurytus sur l'autorité irréprochable d'Archytas. Eurytus était le disciple de Philolaus, et Aristoxenus l'a mentionné avec Philolaus comme ayant enseigné aux derniers pythagoriciens, les hommes qu'il connaissait lui-même. Il appartient donc au début du quatrième siècle avant J.-C., ce qui signifie qu'il n'y a pas eu d'autres changements.à l'époque où le système pythagoricien était pleinement développé, et il n'était pas un enthousiaste excentrique, mais l'un des hommes les plus éminents de l'école. On nous dit donc de lui qu'il avait l'habitude de donner le nombre de toutes sortes de choses, comme les chevaux et les hommes, et qu'il en faisait la démonstration en disposant des cailloux d'une certaine manière. De plus, Aristote compare son procédé à celui de ceux qui transforment les nombres en figures.(schêmata) comme le triangle et le carré.

"Or ces affirmations, et surtout la remarque d'Aristote citée en dernier lieu, semblent impliquer l'existence à cette date, et antérieurement, d'un symbolisme numérique bien distinct de la notation alphabétique d'une part, et de la représentation euclidienne des nombres par des lignes d'autre part. La première était peu commode pour l'arithmétique, car le zéro n'avait pas encore été inventé. La seconde, qui est la représentation des nombres par des lignes, est la représentation des nombres par des lignes.La représentation des nombres par des lignes, adoptée pour éviter les difficultés soulevées par la découverte des quantités irrationnelles, est beaucoup plus tardive. Il semble plutôt que les nombres aient été représentés à l'origine par des points disposés selon des motifs symétriques et facilement reconnaissables, dont le marquage des dés ou des dominos nous donne la meilleure idée. Et ces marquages sont, en fait, la meilleure preuve qu'il s'agit d'uneméthode véritablement primitive d'indication des nombres ; en effet, elles sont d'une antiquité inconnue et remontent à l'époque où les hommes ne pouvaient compter qu'en disposant les nombres selon des schémas dont chacun devenait, en quelque sorte, une nouvelle unité.

"Il est donc significatif que nous ne trouvions aucun indice de ce qu'Aristote entendait par "ceux qui font entrer les nombres dans des figures comme le triangle et le carré" jusqu'à ce que nous arrivions à certains auteurs tardifs qui se sont appelés Pythagoriciens et qui ont fait revivre l'étude de l'arithmétique comme une science indépendante de la géométrie.Nicomaque de Gérasa dit expressément que les lettres utilisées pour représenter les nombres sont purement conventionnelles. La chose naturelle serait de représenter les nombres linéaires ou premiers par une rangée d'unités, les nombres polygonaux par des unités disposées de manière à marquer les différentes figures planes et les nombres solides par des unités.disposés en pyramides et ainsi de suite.

"Il devrait être évident qu'il ne s'agit pas d'une innovation. Bien sûr, l'emploi de la lettre alpha pour représenter les unités est dérivé de la notation conventionnelle, mais pour le reste, nous sommes clairement en présence de quelque chose qui appartient au stade le plus précoce de la science. Nous avons également appris que les points étaient censés représenter des cailloux (psêphoi), ce qui nous éclaire sur les premières méthodes d'analyse de ce qui se passe dans le monde.nous appelons toujours le calcul.

Aetius (394-454) a écrit : "Dix est la nature même du nombre. Tous les Grecs et tous les barbares comptent jusqu'à dix, et après avoir atteint dix, ils reviennent à l'unité. Et encore, Pythagore soutient que la puissance du nombre 10 réside dans le nombre 4, la tétrade. C'est la raison pour laquelle : si l'on part de l'unité (1) et que l'on ajoute les nombres successifs jusqu'à 4, on obtient le nombre 10 (1+2+3+4 = 10).Et si l'on dépasse la tétrade, on dépasse aussi 10..... Ainsi, le nombre par l'unité réside dans le nombre 10, mais potentiellement dans le nombre 4. C'est pourquoi les pythagoriciens avaient l'habitude d'invoquer la tétrade comme leur serment le plus contraignant : "Par celui qui a donné à notre génération la tétrade, qui contient la source et la racine de la nature éternelle..." [Source : Aetius I. 3.8].

"Le fait qu'Aristote s'y réfère semble clair et est confirmé par la tradition selon laquelle la grande révélation faite par Pythagore à l'humanité était précisément une figure de ce type, la tétraktys, par laquelle les pythagoriciens avaient l'habitude de jurer, et nous avons l'autorité de Speusippus pour affirmer que toute la théorie était pythagoricienne.que les pythagoriciens ont juré, était le "tetraktys de la dekad". Il représentait le nombre dix comme le triangle de quatre.

"Il montrait d'un coup d'œil que 1 + 2 + 3 + 4 = 10. Speusippus nous fait part de plusieurs propriétés que les pythagoriciens ont découvert dans le dekad. C'est, par exemple, le premier nombre qui a en lui un nombre égal de nombres premiers et de nombres composés. Nous ne pouvons pas dire dans quelle mesure cela remonte à Pythagore lui-même, mais nous sommes probablement justifiés de lui renvoyer la conclusion selon laquelle il est "selonSource : John Burnet (1863-1928), "Early Greek Philosophy" Londres et Edimbourg : A. et C. Black, 1892, 3ème édition, 1920, Université d'Evansville].

"Il est évident que les tétraktys peuvent être indéfiniment étendus de manière à présenter les sommes des séries de nombres entiers successifs sous une forme graphique, et ces sommes sont en conséquence appelées "nombres triangulaires". Pour des raisons similaires, les sommes des séries de nombres impairs successifs sont appelées "nombres carrés", et celles des nombres pairs successifs "oblongues". Si les nombres impairs sont ajoutés sous la forme de gnomons,il en résulte toujours une figure semblable, à savoir un carré, tandis que, si l'on ajoute des nombres pairs, on obtient une série de rectangles. Il est donc clair que nous sommes en droit de rapporter l'étude des sommes de séries à Pythagore lui-même ; mais nous ne pouvons dire s'il a dépassé l'oblong, et étudié les nombres pyramidaux ou cubiques.

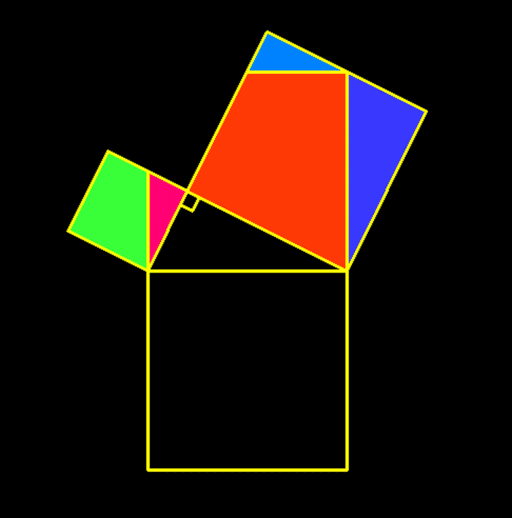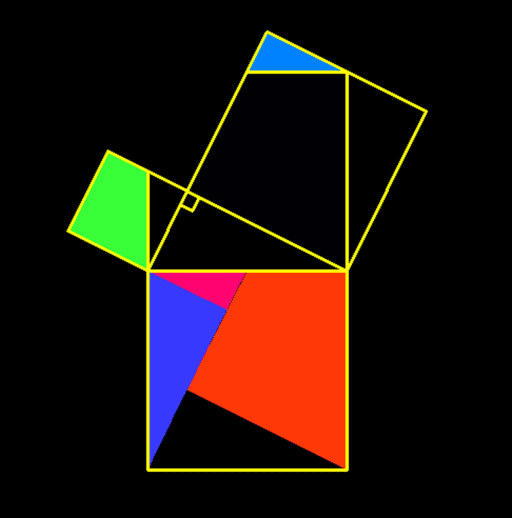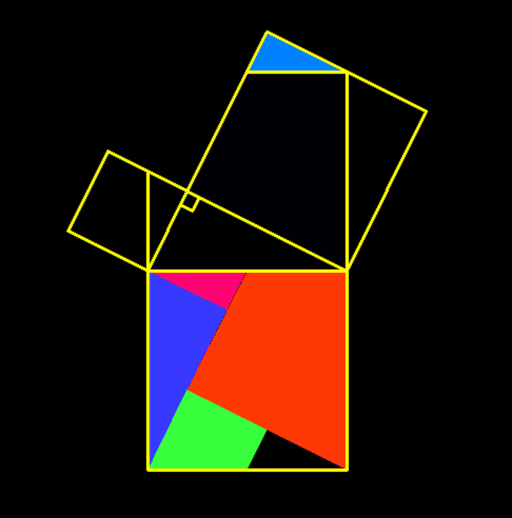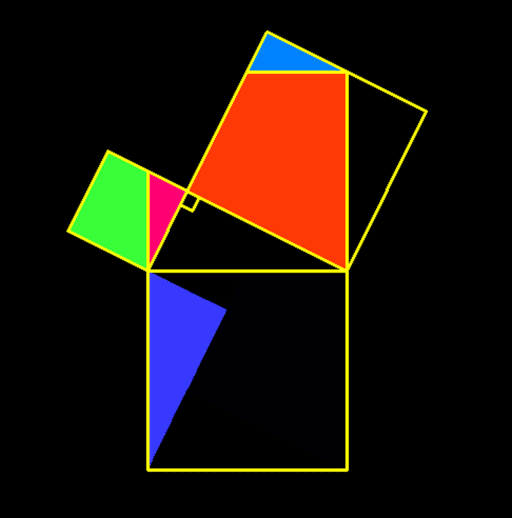
Les points qui représentent les cailloux sont régulièrement appelés "bornes" (horoi, termini, "termes"), et la zone qu'ils délimitent est le "champ" (chôra). Il s'agit manifestement d'une façon ancienne de parler, qui peut être attribuée à Pythagore lui-même. Or, il a dû être frappé par le fait que les "champs" pouvaient être des "bornes".Il connaissait, bien sûr, l'usage du triangle 3, 4, 5 dans la construction des angles droits. Nous avons vu (§ XI) qu'il était familier en Orient depuis un certain temps.Or, la proposition pythagoricienne par excellence est que, dans un triangle rectangle, le carré de l'hypoténuse est égal aux carrés des deux autres côtés, et que le triangle dit de Pythagore est l'application de cette proposition.Le nom même d'"hypoténuse" (hupoteinousa) confirme fortement le lien intime entre les deux choses. Il signifie littéralement "la corde qui s'étend à l'opposé", et il s'agit certainement de la corde de l'"arpédonapt". Il est donc tout à fait possible que cette proposition ait été réellement découverte par Pythagore, bien que nous ne puissions en être sûrs, et bien que le nom de l'"arpédonapt" ne soit pas le même que celui de l'"arpédonapt".la démonstration qu'en donne Euclide n'est certainement pas la sienne [Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3rd edition, 1920, Evansville University].

"Une grande déception, cependant, l'attendait. Il découle immédiatement de la proposition pythagoricienne que le carré de la diagonale d'un carré est le double du carré de son côté, ce qui devrait sûrement pouvoir être exprimé arithmétiquement. En fait, il n'existe aucun nombre carré qui puisse être divisé en deux nombres carrés égaux, et le problème ne peut donc pas être résolu. Dans ce cas, le problème n'est pas résolu.En ce sens, il est peut-être vrai que Pythagore a découvert l'incommensurabilité de la diagonale et du côté d'un carré, et la preuve mentionnée par Aristote, à savoir que, s'ils étaient commensurables, nous devrions dire qu'un nombre pair est égal à un nombre impair, a un caractère nettement pythagoricien.Il a peut-être trébuché sur le fait que la racine carrée de deux est un surd, mais nous savons qu'il a été laissé aux amis de Platon, Théodore de Cyrène et Théétète, le soin de donner une théorie complète des irrationnels. Pour le moment, l'incommensurabilité de la diagonale et du carré est restée, comme on l'a dit, une "exception scandaleuse". Notre tradition dit qu'Hippasus de Métaponte s'est noyé en mer.pour avoir révélé ce squelette dans le placard.

"Ces dernières considérations montrent que, s'il est tout à fait sûr d'attribuer la substance des premiers livres d'Euclide aux premiers pythagoriciens, sa méthode arithmétique n'est certainement pas la leur. Elle opère avec des lignes au lieu d'unités, et elle peut donc être appliquée à des relations qui ne sont pas susceptibles d'être exprimées comme des équations entre des nombres rationnels. C'est sans doute la raison pour laquelle l'arithmétique estPour la même raison, la doctrine de la proportion que nous trouvons dans Euclide ne peut pas être pythagoricienne, et est en fait l'œuvre d'Eudoxe. Pourtant, il est clair que les premiers pythagoriciens, et probablement Pythagore lui-même, ont étudié la proportion à leur manière, et que les trois "médieties" (mesotêtes) en particulier vont dans le sens de la proportion.Si nous prenons la proportion harmonique 12:8:6, nous constatons que 12:6 est l'octave, 12:8 la quinte et 8:6 la quarte, et il ne fait guère de doute que c'est Pythagore lui-même qui a découvert ces intervalles. On raconte qu'il aurait observé les intervalles harmoniques dans une forge,et de peser les marteaux qui les ont produits, ou de suspendre à des cordes égales des poids correspondant à ceux des marteaux, sont certes impossibles et absurdes, mais c'est une pure perte de temps que de les rationaliser. Pour notre propos, leur absurdité est leur principal mérite. Ce ne sont pas des histoires qu'aucun mathématicien grec n'aurait pu inventer, mais des contes populaires qui témoignent de l'existence d'un système d'information et de communication.En revanche, l'affirmation selon laquelle Pythagore aurait découvert les "consonances" en mesurant les longueurs correspondantes sur le monocorde est tout à fait crédible et ne comporte aucune erreur d'acoustique.

" Les pythagoriciens, selon Aristoxène, pratiquaient la purification (catharsis) du corps par la médecine, et de l'âme par la musique " [Source : Cramer, Anthologie de Paris I. 172].

Les pythagoriciens ont montré comment les nombres pouvaient être utilisés pour décrire les harmonies et les beautés de la musique et ont introduit la terminologie musicale de l'octave, de la quinte, du quart, exprimés par 2:1, 3:1 et 4:3. Ils ont constaté que les sons les plus agréables se produisaient dans des proportions exactes et ont découvert que la longueur d'une corde musicale était en relation numérique exacte avec la hauteur de son ton.

Les notes sont des ondes sonores créées par des vibrations. Une vibration qui est deux fois plus élevée qu'une autre est une octave. D'autres qui sont agréables ensemble sont celles dont la vibration est supérieure d'un quart ou d'une quinte. Ces mêmes proportions sont utilisées dans la conception de ce qui est considéré comme un bâtiment esthétiquement agréable, c'est pourquoi l'architecture a été appelée "musique figée".

En décrivant les pythagoriciens dans sa Métaphysique, Aristote écrit : "ils disent que les choses elles-mêmes sont des nombres et ne placent pas les objets des mathématiques entre les formes et les choses sensibles... Puisque, encore une fois, ils ont vu que les modifications et les rapports de la musique...".les échelles étaient exprimables en nombres - puisque, alors, toutes les autres choses semblaient dans leur nature entière, ils ont supposé que les éléments des nombres étaient les éléments de toutes choses, et que le ciel entier était une échelle musicale et un nombre... et l'arrangement entier des cieux, ils l'ont recueilli et l'ont adapté à leur schéma ; et s'il y avait une lacune quelque part, ils ont volontiers fait des ajouts de façon à rendre leur ensemble...théorie cohérente."

Nous verrons qu'à une date ultérieure, les pythagoriciens ont identifié ces nombres avec des figures géométriques ; mais le simple fait qu'ils les aient appelés "nombres", en relation avec ce qui nous est dit de la méthode d'Eurytus, suffit à montrer que ce n'était pas le sens originel de la doctrine. Il suffit de supposer que le mot "nombres" n'a pas été utilisé par les pythagoriciens.Si les sons musicaux peuvent être réduits à des nombres, pourquoi pas tout le reste ? Il y a beaucoup de similitudes avec les nombres dans les choses, et il se pourrait bien qu'une expérience heureuse, comme celle qui a permis de découvrir l'octave, révèle leur véritable nature numérique. Les auteurs néopythagoriciens, remontant sur ce point comme sur d'autres à la plus ancienne tradition de l'histoire de l'humanité, ont dit que les nombres étaient un élément essentiel de la vie.Aristote nous dit distinctement que les pythagoriciens n'expliquaient que quelques choses par les nombres, ce qui signifie que Pythagore lui-même n'a pas laissé de doctrine développée à ce sujet, tandis que les pythagoriciens du cinquième siècle n'en ont pas laissé d'autres.Aristote laisse toutefois entendre que, selon eux, le "bon moment" (kairos) était de sept, la justice de quatre et le mariage de trois. Ces identifications, ainsi que quelques autres du même genre, peuvent être attribuées sans risque à Pythagore ou à ses successeurs immédiats ; mais nous ne devons pas leur accorder trop d'importance.Nous pouvons trouver des déclarations qui présentent des points de contact avec l'enseignement de l'école de Milésia. Nous pouvons raisonnablement en déduire qu'elles appartiennent au système dans sa forme la plus primitive. [Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3rd edition, 1920, Evansville University ].

Les pythagoriciens de l'époque de Socrate ont adapté les idées pythagoriciennes sur les nombres à la nouvelle théorie des "éléments". C'est ce qui rend nécessaire la reprise de l'examen du système en relation avec les pluralistes. Lorsque les pythagoriciens sont retournés dans le sud de l'Italie, ils y ont trouvé des points de vue qui exigeaient une reconstruction partielle de leur propre système. Nous ne savons pas si les pythagoriciens ont été capables d'adapter leur système.Empédocle a fondé une société philosophique, mais son influence sur l'école de médecine de ces régions ne fait aucun doute ; et nous savons aussi maintenant que Philolaus a joué un rôle dans l'histoire de la médecine. Cela nous donne la clé de ce qui semblait auparavant obscur. La tradition veut que les Pythagoriciens aient expliqué les éléments comme étant constitués de figures géométriques, une théorie que nous pouvons étudier par nous-mêmes dansS'ils voulaient conserver leur position de leaders dans l'étude de la médecine en Italie, ils étaient obligés de rendre compte des éléments [Source : John Burnet (1863-1928), "Early Greek Philosophy" London and Edinburgh : A. and C. Black, 1892, 3rd edition, 1920, Evansville University].

"Il ne faut pas croire, cependant, que la construction pythagoricienne des éléments était exactement la même que celle que nous trouvons dans le Timée de Platon. Comme nous l'avons vu, il y a de bonnes raisons de croire qu'ils ne connaissaient que trois des solides réguliers, le cube, la pyramide (tétraèdre) et le dodécaèdre. Or Platon fait partir le Timée du feu et de la terre, et dans la construction des éléments ilIl s'ensuit que si l'air et l'eau se transforment facilement en feu, la terre ne le peut pas, et le dodécaèdre est réservé à un autre usage, que nous verrons plus loin. Cela conviendrait parfaitement au système pythagoricien, car il laisserait de la place à l'eau et au feu.Nous savons qu'Hippasus a fait du feu le premier principe, et nous voyons dans le Timée comment il serait possible de représenter l'air et l'eau comme des formes du feu. L'autre élément est cependant la terre, et non l'air, comme nous avons des raisons de croire qu'il l'était dans le pythagorisme primitif. Ce serait un résultat naturel de la découverte de l'élément de la terre.Cela expliquerait aussi le fait étonnant, que nous avons dû laisser inexpliqué plus haut, qu'Aristote identifie les deux "formes" dont parle Parménide avec le feu et la terre.

"Le point le plus intéressant de la théorie est cependant l'utilisation du dodécaèdre. Il était identifié, nous dit-on, à la "sphère de l'univers" ou, comme le dit le fragment de Philolaic, à la "coque de la sphère". Quoi que l'on puisse penser de l'authenticité des fragments, il n'y a aucune raison de douter qu'il s'agit d'une expression pythagoricienne authentique, et elle doit être prise en compte de près.La structure du monde était comparée à la construction d'un navire, une idée dont on trouve d'autres traces. La clé de ce qui nous est dit sur le dodécaèdre nous est également donnée par Platon. Dans le Phédon, qui a dû être écrit avant que la doctrine des solides réguliers ne soit pleinement établie, nous lisons que la "vraie terre", si elle est regardée depuis le centre de l'Europe, est une terre qui n'a pas été construite à partir de l'Europe.ci-dessus, est "multicolore comme les balles qui sont faites de douze pièces de cuir".

"L'opinion selon laquelle l'âme est une "harmonie", ou plutôt une syntonisation, est intimement liée à la théorie des quatre éléments. Elle ne peut pas avoir appartenu à la forme la plus ancienne du pythagorisme, car, comme le montre le Phédon de Platon, elle est tout à fait incompatible avec l'idée que l'âme peut exister indépendamment du corps. C'est le contraire même de la croyance selon laquelle "toute âme peut entrer dans tout corps".D'autre part, le Phédon nous dit qu'elle a été acceptée par Simmias et Cébès, qui avaient entendu Philolaus à Thèbes, et par Echecrate de Phlius, qui était le disciple de Philolaus et d'Eurytus. Le récit de la doctrine donné par Platon est tout à fait conforme à l'idée qu'elle était d'origine médicale. Simmias dit : " Notre corps étant, pour ainsi dire, ficelé et maintenu ensemble par le chaud et le froid, le sec et le froid ".Si donc notre âme est un accord, il est clair que, lorsque le corps est détendu ou démesuré par les maladies et autres maux, l'âme doit nécessairement périr immédiatement.Il complète la preuve que le pythagorisme de la fin du Ve siècle était une adaptation de l'ancienne doctrine aux nouveaux principes introduits par Empédocle.

"Il faut en outre observer que, si l'on considère l'âme comme une syntonie au sens pythagoricien, on doit s'attendre à ce qu'elle contienne les trois intervalles alors reconnus, la quarte, la quinte et l'octave, ce qui rend extrêmement probable que Posidonius avait raison de dire que la doctrine de l'âme tripartite, telle que nous la connaissons par la République de Platon, était réellement pythagoricienne...".Il est tout à fait incompatible avec l'idée que Platon se fait de l'âme, mais s'accorde admirablement avec celle qui vient d'être expliquée.

"Le système planétaire qu'Aristote attribue aux "pythagoriciens" et Aetius à Philolaus est suffisamment remarquable. La terre n'est plus au milieu du monde ; sa place est occupée par un feu central, qui ne doit pas être identifié avec le soleil. Autour de ce feu tournent dix corps. D'abord vient l'Antichthon ou Contre-Terre, et ensuite la terre, qui devient ainsi une des planètes.Après la terre vient la lune, puis le soleil, les planètes, et le ciel des étoiles fixes. Nous ne voyons pas le feu central et l'antickthon parce que le côté de la terre sur lequel nous vivons en est toujours détourné. Cela s'explique par l'analogie de la lune, qui nous présente toujours la même face, de sorte que les hommes vivant de l'autre côté d'elle ne verraient jamais la terre.implique, bien sûr, de notre point de vue, que ces corps tournent sur leurs axes en même temps qu'ils tournent autour du feu central, et que l'antichthon tourne autour du feu central en même temps que la terre, de sorte qu'il est toujours en opposition avec lui.

musique des sphères

"Il n'est pas facile d'accepter l'affirmation d'Aetius selon laquelle ce système a été enseigné par Philolaus. Aristote ne le mentionne nulle part en rapport avec ce système, et dans le Phédon, Socrate donne une description de la terre et de sa position dans le monde qui lui est entièrement opposée, mais qui est acceptée sans démenti par Simmias, le disciple de Philolaus. Cependant, il s'agit indubitablement d'une théorie pythagoricienne, et elle marque un tournant dans l'histoire de l'humanité.Il est également clair que Socrate considère comme une nouveauté le fait que la terre n'a pas besoin du soutien de l'air ou de quoi que ce soit d'autre pour rester à sa place. Même Anaxagore n'avait pas pu se défaire de cette idée, et Démocrite la soutenait encore avec la théorie de la terre plate. La déduction naturelle du Phédon est la suivanteIl est certain que la théorie d'une terre sphérique, maintenue au milieu du monde par son équilibre, est celle de Philolaus lui-même. Si tel est le cas, la doctrine du feu central appartiendrait à une génération ultérieure.

"Il semble probable que la théorie de la révolution de la terre autour du feu central a réellement pris naissance dans le récit de la lumière du soleil donné par Empédocle. Les deux choses sont mises en relation étroite par Aetius, qui dit qu'Empédocle croyait à deux soleils, tandis que "Philolaus" croyait à deux ou même à trois soleils. Ses paroles sont obscures, mais elles semblent nous justifier de tenir pour Théophraste.Nous avons vu qu'Empédocle donnait deux explications contradictoires de l'alternance du jour et de la nuit (§ 113) et il a pu sembler que la solution de la difficulté consistait à faire briller le soleil par la lumière réfléchie d'un feu central. Une telle théorie serait, en fait, l'aboutissement naturel des découvertes récentes sur la lumière de la lune et la cause de ses éclipses, si ces découvertes ont été faites.ont été étendus au soleil, comme ils le seraient presque inévitablement.

"Le feu central a reçu un certain nombre de noms mythologiques, tels que le "foyer du monde", la "maison" ou la "tour de guet" de Zeus, et la "mère des dieux". C'était dans les habitudes de l'école, mais cela ne doit pas nous faire oublier que nous avons affaire à une hypothèse scientifique. C'était une grande chose de voir que les phénomènes pouvaient être "sauvés" au mieux par un luminaire central, et que la terreIl est probable, en tout cas, que cette théorie a été à l'origine de la réflexion qui a permis à Aristarque de Samos d'aboutir à l'hypothèse héliocentrique, et c'est certainement la réaffirmation réussie par Aristote de la théorie de l'héliocentrisme.Nous avons sa propre parole pour dire qu'il est parti de ce qu'il avait lu sur les pythagoriciens.

Sources des images : Wikimedia Commons

Sources du texte : Stanford Encyclopedia of Philosophy /plato.stanford.edu, Internet Encyclopedia of Philosophy iep.utm.edu ; Internet Ancient History Sourcebook : Greece sourcebooks.fordham.edu ; Internet Ancient History Sourcebook : Hellenistic World sourcebooks.fordham.edu ; BBC Ancient Greeks bbc.co.uk/history/ ; Musée canadien de l'histoire historymuseum.ca ; Perseus Project - Tufts University ;perseus.tufts.edu ; MIT, Online Library of Liberty, oll.libertyfund.org ; Gutenberg.org gutenberg.org Metropolitan Museum of Art, National Geographic, Smithsonian magazine, New York Times, Washington Post, Los Angeles Times, Live Science, Discover magazine, Times of London, Natural History magazine, Archaeology magazine, The New Yorker, Encyclopædia Britannica, "The Discoverers" [∞] et "TheTime, Newsweek, Wikipedia, Reuters, Associated Press, The Guardian, AFP, guides Lonely Planet, "World Religions" édité par Geoffrey Parrinder (Facts on File Publications, New York) ; "History of Warfare" par John Keegan (Vintage Books) ; "History of Art" par H.W. Janson Prentice Hall, Englewood Cliffs,N.J.), Compton's Encyclopedia et divers livres et autres publications.

---